Парадокс Монти Холла
— «Видел видео?»
— «Какое?»
— «Я вообще не понимаю как такое возможно…»
И понеслось.
Немного о том, что из себя представляет парадокс:
Представьте, что вы стали участником игры, в которой вам нужно выбрать одну из трёх дверей. За одной из дверей находится автомобиль, за двумя другими дверями — козы. Вы выбираете одну из дверей, например, номер 1, после этого ведущий, который знает, где находится автомобиль, а где — козы, открывает одну из оставшихся дверей, например, номер 3, за которой находится коза. После этого он спрашивает вас — не желаете ли вы изменить свой выбор и выбрать дверь номер 2? Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор?
Источник: Педивикия
Сначала рассмотрим классическую формулировку парадокса, т.е. всего 3 двери.
| Дверь 1 | Дверь 2 | Дверь 3 | Менять выбор | Не менять выбор | |
|---|---|---|---|---|---|
| Вариант 1 | Автомобиль 🚗 | Козел 🐐 | Козел 🐐 | 0 | 1 |
| Вариант 2 | Козел 🐐 | Автомобиль 🚗 | Козел 🐐 | 1 | 0 |
| Вариант 3 | Козел 🐐 | Козел 🐐 | Автомобиль 🚗 | 1 | 0 |
| ≈0.667 | ≈0.334 |
Первым делом выбираем дверь. В нашей таблице выбор всегда падает на дверь 1.
Если за первой дверью скрывалась машина, то менять свой выбор явно не стоит. Но такая ситуация встречается лишь один раз. В остальных случаях — смена выбора принесет нам победу. Почему так происходит? Все из-за того, что ведущий откроет дверь с козлом. В вариантах 2 и 3, ведущий тем самым оставит нам дверь в автомобилем. Нам останется (в варианте 2 и 3) сменить выбор на автомобиль.
Т.е. для ситуации, когда мы меняем выбор — у нас две выигрышные позиции (из трех), когда мы не меняем — у нас одна выигрышная позиция . Из чего следует, что вероятность выигрыша, если мы меняем выбор, наивысшая и равна 0.66.
Отлично. С тремя дверями разобрались. Как дела обстоят с 4, 5, 8 … 100?
Чтобы было проще создать модель, по который мы будем вычислять, составим таблицу с четырьмя дверями:
| Дверь 1 | Дверь 2 | Дверь 3 | Дверь 4 | Менять выбор | Не менять выбор | |
|---|---|---|---|---|---|---|
| Вариант 1 | Автомобиль 🚗 | Козел 🐐 | Козел 🐐 | Козел 🐐 | 0 | 1 |
| Вариант 2 | Козел 🐐 | Автомобиль 🚗 | Козел 🐐 | Козел 🐐 | 0.5 | 0 |
| Вариант 3 | Козел 🐐 | Козел 🐐 | Автомобиль 🚗 | Козел 🐐 | 0.5 | 0 |
| Вариант 4 | Козел 🐐 | Козел 🐐 | Козел 🐐 | Автомобиль 🚗 | 0.5 | 0 |
| 0.375 | 0.25 |
Теперь, если автомобиль оказался не за первой дверью (которую мы выбираем), вероятность выиграть стала 0.5. Не сложно посчитать что общая вероятность выиграть теперь: \(\frac{1}{0.5 * 3} = 0.375\)
Составим формулу, по которой сможем смело вычислять вероятность выигрыша, если мы меняем выбор:
$$P(A)=\frac{d-1}{(d-2)*d}$$
где A — событие выигрыша, d — количество дверей.
Если мы не меняем выбор: \[P(A)=\frac{1}{d}\]
А теперь самое интересное. Напишем программу, которая будет проводить вычисления быстро и красиво.
// Вычисление вероятности выигрыша по
// парадоксу Монти Холла
#include <iostream>
using namespace std;
int main() {
int doors;
// Ввод
printf("Doors: ");
scanf("%d", &doors);
// Вычисления
double q = 1.0f / (doors - 2);
double a = (q * (doors - 1)) / doors;
double b = 1.0f / doors;
// Ответ
printf("change: %f / not change: %f", a, b);
return 0;
}
// by @mvodya with @ProudKingLion
Немного поигравшись программой, узнаем:
- Если дверей будет 5, вероятность выиграть при смене выбора: ≈0.2667, при сохранении: 0.2
- Если дверей будет 8, вероятность выиграть при смене выбора: ≈0.145833, при сохранении: 0.125
- Если дверей будет 15, вероятность выиграть при смене выбора: ≈0.071795, при сохранении: ≈0.066667
- Если дверей будет 100, вероятность выиграть при смене выбора: ≈0.010102, при сохранении: 0.01
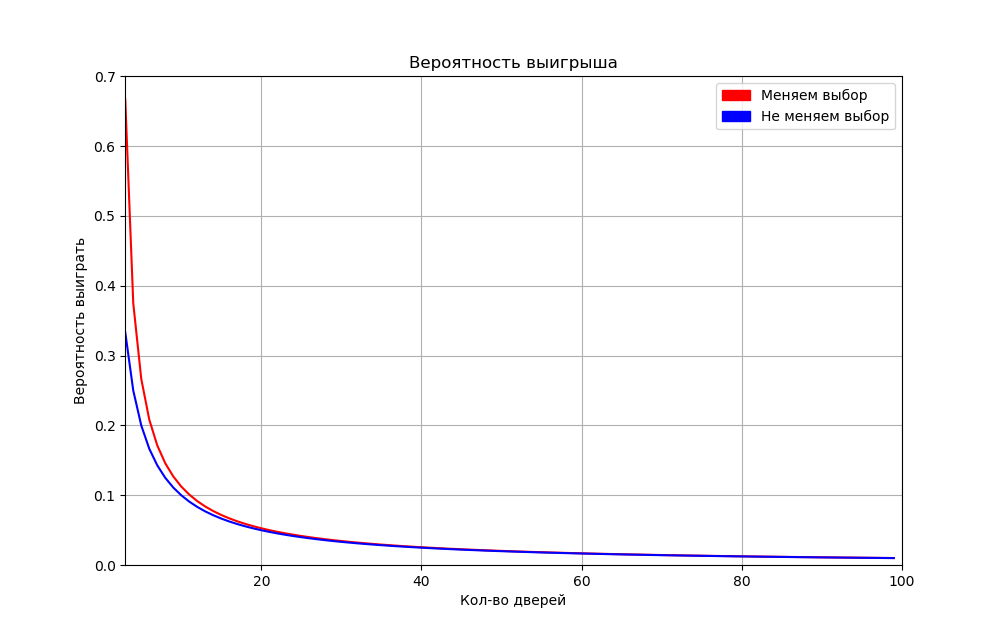
Из сего выясняем очевидную вещь: чем больше дверей, тем меньше наш выбор влияет на возникновение благоприятного события.